Saludo.

Hola estimados usuarios les saludan los estudiantes de la carrera de ingeniería en sistemas automatizados de la Universidad Evangélica Nicaragüense UENIC-Masaya. Este blog trata con lo que tiene que ver en la asignatura de Álgebra y las transformaciones del plano, con el fin de que su contenido les sea de mucha utilidad y agrado. Gracias por visitar nuestro Blog. Dios le bendiga!. 

Conceptos Básicos de la Asignatura.

Relación Suprayectiva: Es la aplicación sobre dos conjuntos cualquiera que no necesariamente tienen la misma cardinalidad y habrá menos elementos del conjunto de partida sin imagen.

Relación Inyectiva: es aquella aplicación en donde el conjunto de llegada es de mayor cardinalidad que el conjunto de partida.

Relación o aplicación Biyectiva: es aquella que es Suprayectiva e inyectiva a la vez.

Grupo: es un conjunto de elementos para los que esta definido una operación algebraica.

Transformación del plano: es una aplicación biyectiva del plano sobre si mismo.

Movimiento del plano: es una transformación que no cambia la distancia y se denota con “M”.

Propiedades del M del plano:

1-    M transforma una recta en otra recta.

2-    M transforma un semiplano con frontera A en otro Semiplano con frontera A prima (A’).

3-    M guarda la relación start entre.

4-    M transforma un segmento en otro segmento.

5-    Un rayo en otro rayo

6-    Un ángulo a otro ángulo  igual al primero.

7-    Rectas perpendiculares en rectas perpendiculares. 

Congruencia: Es una figura L', es congruente a una figura dada L, si existe un movimiento del plano que transforma L en L'. Se lee L es congruente de L'.

Deslizamiento.

En el deslizamiento tenemos al vector y rosa de los vientos. 

Un vector (también llamado vector euclidiano o vector geométrico) es una magnitud física definida en un sistema de referencia que se caracteriza por tener módulo (o longitud) y una dirección (u orientación).

Rosa de los vientos es un símbolo en forma de círculo que tiene marcados alrededor los rumbos en que se divide la circunferencia del horizonte. Su invención se atribuye al mallorquín Ramón Llull, aunque la descripción pormenorizada que da Plinio el viejo en libro II¹​ podría haber sido su referencia básica.

Como trazar una Simetría Central.

Simetría Central.

Definición:

La simetría central, de este modo, se considera a partir de un punto que se conoce como centro de simetría. Todos los puntos correspondientes en una simetría central se denominan puntos homólogos y permiten trazar segmentos homólogos que son iguales y que disponen de ángulos correspondientes que también miden igual. 

Dicho de otro modo, los puntos A y A’ son simétricos respecto a un centro de Simetría S cuando SA y SA’, siendo A y A’ equidistantes de S. Es importante destacar que SA y SA’ disponen de la misma longitud.

Como trazar una Simetría Axial.

Simetría Axial.

Definición:

Se conoce como simetría axial a la simetría que existe en torno a un eje cuando la totalidad de los semiplanos que se toman desde una determinada mediatriz exhiben las mismas características.

Para determinar si existe simetría axial, se considera que los puntos que pertenecen a una figura sean coincidentes con los puntos que forman parte de otra figura, tomando a modo de referencia el eje de simetría (una línea). De esta manera, la simetría axial supone un fenómeno similar al que ocurre cuando un espejo refleja una imagen.

Rotación.

Definición: Es un movimiento alrededor de un punto que mantiene la forma y el tamaño de la figura original.

Una rotación se determina por estos tres elementos:

·        Un ángulo que determina la amplitud de la rotación.

·        Un punto llamado centro de rotación.

·    Un sentido de la rotación que puede ser del mismo sentido de las agujas del reloj o en sentido contrario.

La vida cotidiana está llena de situaciones en las que la rotación o giro está presente. Cuando abrimos o cerramos una puerta estamos haciendo una rotación sobre un punto o centro de rotación, las ruedas de nuestra bicicleta giran sobre el eje central, al igual que los pedales, giramos al montarnos a los caballitos, al abrir y cerrar el abanico hacemos que gire sobre un punto al mover la ruleta hacemos que gire igualmente sobre su centro 

Trazado de una Homotecia

Propiedades de la Homotecia.

1.    El único punto invariante de una homotecia es el centro de homotecia.
2.   Las rectas que pasan por el centro de homotecia son rectas invariantes.
3.   Las rectas que contienen segmentos homólogos son paralelas, y la razón de dichos segmentos coincide con la razón de homotecia.
4.  Una homotecia conserva el sentido de las figuras.
5. Una homotecia de razón k = 1 transforma cada punto en sí mismo. Recibe el nombre de Identidad.
6. Si la razón de homotecia es k = - 1, se trata de una simetría central.

Tipos de Homotecia

Homotecia Directa:

La razón es positiva, es decir k > 0.

las figuras quedan a un mismo lado de la homotecia

Homotecia inversa:

 La razón es negativa, es decir k < 0.

Las figuras se encuentran en lados opuestos con respecto al centro de la homotecia. 

Definición de Homotecia.

Homotecia.

Una homotecia es una transformación geométrica que, a partir de un punto fijo, multiplica todas las distancias por un mismo factor.

Además permite ampliar o reducir el tamaño de una figura conservando la medida de los ángulos y manteniendo constante la razón de los lados.

Se define Homotecia de centro O y razón k a la transformación que hace corresponder a un punto P otro punto P’, alineado con P y O, tal que:

d (O, P’) = k * d (O, P).

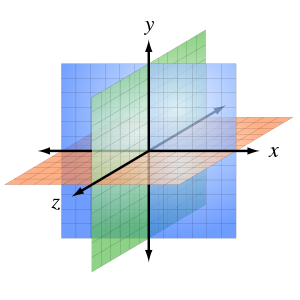
Tipos de gráficos tridimensional.

4. Gráficos de indicadores.

5. Gráficos de líneas.

 6.  Gráficos circulares y de anillos.

7. Gráficos de dispersión, de puntos y burbujas.

Tipos de gráficos tridimensionales.

Tipos de gráficos tridimensionales.

1.       Gráficos de área.

2.       Gráficos de barra.

3.       Gráficos de columnas.

Gráficos tridimensionales.

Gráficos Tridimensionales.

Los gráficos tridimensionales ofrecen una imagen visualmente efectiva que resulta adecuada para las presentaciones.

Los gráficos de columnas, barras, líneas y de áreas tridimensionales trazan los datos usando tres ejes.

No use gráficos tridimensionales cuando deba mostrar valores exactos, como los destinados a tareas de control o de supervisión. La distorsión en los gráficos tridimensionales puede dificultar su lectura precisa. Por ejemplo, el gráfico siguiente muestra los ingresos reales de cada línea de producto en cada territorio; sin embargo, algunas etiquetas de datos se omiten dado que no hay espacio suficiente para mostrarlas todas.

Otros tipos de Construcciones de Volutas

Voluta de tres centros.

Sea p el paso de la voluta.

1. Construimos un triángulo equilátero de lado p/3. Los vértices del triángulo son los centros de los arcos de circunferencia.

2. Prolongamos los lados de la forma que vemos en la fig., formando ángulos de 120º pues como tenemos tres centros (3x120º =360º) se completa una vuelta completa.

3. Con centro en A trazamos el arco de radio AB obteniendo el punto 1.

 4. Con centro en B trazamos el arco de radio B1 obteniendo el punto 2.

 5. Con centro en C trazamos el arco de radio C2 obteniendo el punto 3.

 6. Con centro en A trazamos el arco de radio A3 obteniendo el punto 4.

7. La distancia de 1 a 4 es la distancia p del paso dado

8. Continuamos trazando arcos de circunferencia de centros en A, B y C respectivamente. 

Voluta de cuatro centros.

Sea p el paso de la voluta.

1. Construimos un cuadrado ABCD de lado p/4 (el paso dividido por cuatro).Los vértices del cuadrado son los centros de los arcos de la circunferencia. Hallamos la mediatriz del paso dado y obtenemos el punto O.

2. Prolongamos los lados de la forma que vemos en la fig., formando ángulos de 90º pues como tenemos cuatro centros (4x90º =360º) se completa una vuelta completa.

3. Con centro en B trazamos el arco de radio BA obteniendo el punto 1.

4. Con centro en C trazamos el arco de radio C1 obteniendo el punto 2.

5. Con centro en D trazamos el arco de radio D2 obteniendo el punto 3.

6. Con centro en A trazamos el arco de radio A3 obteniendo el punto 4.

7. La distancia de A-4=1-5 es la distancia p del paso dado  

8. Continuamos trazando arcos de circunferencia de centros en A, B, C y D respectivamente.

Volutas.

Volutas

Definición: Se denomina voluta a la curva plana, abierta y continúa compuesta por arcos de circunferencia, tangentes entre sí, siendo los centros de los arcos los vértices de un polígono básicamente regular. Se denomina paso a la distancia que existe entre dos puntos distanciados entre si una vuelta.

Construcción de volutas A continuación se desarrollan algunos de los trazados de volutas más utilizados en dibujo técnico. Pero prácticamente cada polígono tiene una voluta. Las volutas pueden considerarse evolventes del polígono correspondiente.

Voluta de dos centros

Sea p el paso de la voluta.

 1. Trazamos una recta, sobre la recta llevamos el paso p.

 2. Hallamos la mediatriz del paso dado y obtenemos el punto O.

3. Con centro en C trazamos el arco de circunferencia de radio OA=OB=p/2 (la mitad del paso dado). Los puntos O y A son los centros de la voluta.

 4. Con centro en A trazamos el arco de radio AB obteniendo el punto 1.

 5. Con centro en O trazamos el arco de radio O1 obteniendo el punto 2. 

6. Continuamos trazando arcos de circunferencia de centros en O y en A alternativamente las veces necesarias.

Construcción de espiral.

Construcción de espirales.

 A continuación, se desarrollan algunos de los trazados de espirales más utilizados en dibujo técnico.

Espiral de Arquímedes conociendo el paso OM.

1. Se divide el segmento OM en un número cualquiera de partes iguales, por ejemplo dieciséis. Con centro en O y con radios O1, O2..., hasta O16, se trazan circunferencias.

 2. Se divide la circunferencia en dieciséis partes iguales y se trazan los respectivos radios. Las intersecciones de dichos radios con los arcos correspondientes determinan los diversos puntos que configuran la espiral, puntos que, unidos con trazo continuo, determinan la curva pedida.

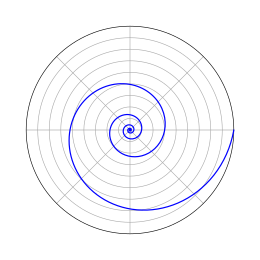
Espiral

Espiral.

Definición: La espiral es una curva plana, abierta y continua que se configura en expansión por un punto que se desplaza de manera uniforme a lo largo de una recta, estando ésta fija en un punto por el cual gira con un valor angular constante. Una espiral se define por los siguientes elementos: Paso: es la distancia longitudinal con que se desplaza un punto de la curva en una vuelta completa. Es decir, es la distancia entre dos espiras consecutivas.

Espira: es la parte de la curva descrita en cada vuelta.

Núcleo: es a partir de donde se genera, en expansión, la espiral. Los núcleos pueden ser lineales si los centros están situados en una línea, o poligonales si son los vértices del polígono los centros que generan la curva.

Radios vectores: son la prolongación, bien de la línea donde están situados los centros del núcleo, o bien de los lados del polígono que hace de núcleo. 

Ovoide según el eje mayor

Ovoide conociendo el eje mayor.

 1. Se divide el eje mayor AB en seis partes iguales, y por la segunda división se traza una perpendicular al eje. Se hace centro en esa misma división, es decir en la 2, y con radio 2-6, se describe un arco que determina los puntos O3 y O4.

 2. Se unen O3 y O4 con el punto 5, quinta división de AB. Se hace centro en el punto 2 y con radio 2A se dibuja una semicircunferencia, obteniendo sobre el segmento O3-O4 los puntos D y C. Con centro en O3 y O4, respectivamente, y radio O3-C=O4-D, se trazan los arcos que determinan los puntos E y F.

 3. Por último, con centro en el punto 5, y con radio 5-B se traza un arco para terminar de construir el ovoide pedido.

Ovoide

Ovoide

 Definición: El ovoide es una curva plana y cerrada, simétrica sólo respecto a su eje mayor, y formada por cuatro arcos de circunferencia, de los que dos son iguales y los otros dos son desiguales. El ovoide tiene dos ejes perpendiculares entre si uno llamado eje mayor y otro llamado eje menor que es un diámetro de uno de sus arcos y su mediatriz es el eje mayor.

Construcción de ovoides

 A continuación, se desarrollan algunos de los trazados de ovoides más utilizados en dibujo técnico.

 Ovoide conociendo el eje menor

 1. Se dibuja la mediatriz del eje conocido AB, obteniendo el punto O1. Con centro en O1 y radio O1A, se traza una circunferencia que corta a la mediatriz en el punto O2, que resulta ser otro centro del ovoide.

 2. Se unen los puntos A y B con O2, obteniendo las semirrectas A-O2 y B-O2. Se trazan dos arcos con radio AB y centro en los puntos A y B, obteniéndose así los puntos 1 y 2. 3. Con centro en O2 y radio O2-1 o O2-2, se describe el último arco que configura el ovoide pedido.

Ovalo según el eje mayor

 Óvalo conociendo el eje mayor

1. Se divide el eje mayor AB en tres partes iguales, determinando así los puntos O1 y O2. Con centro en estos puntos y radio igual a 1/3 de AB, por ejemplo, OA, se trazan dos circunferencias que se cortan en los puntos O3 y O4.

 2. Se unen mediante rectas los puntos O1 y O2 con O3 y O4, obteniendo así los cuatro puntos de tangencia: C y D, y E y F.

3. Con centro en O3 y O4 respectivamente y radio O3E, se realizan dos arcos hasta unir los puntos E con F y C con D. De este modo queda resuelto el óvalo pedido.

Óvalo conociendo el eje mayor.

1. Se divide el eje mayor AB en cuatro partes iguales, obteniendo así los puntos O1 y O2 que corresponden a los puntos 1 y 3 en el eje dividido. Se trazan dos circunferencias con centro en O1 y O2, respectivamente, y radio igual a 1/4 de AB, es decir, O1A.

 2. Se trazan dos arcos con centro también en O1 y O2, respectivamente, y radio igual a O1-O2.

 3. Donde los arcos se cortan se encuentran los puntos O3 y O4, centros de los arcos mayores del óvalo. Para hallar los puntos de tangencia se unen los centros O3 y O4 con los otros centros O1 y O2, y a partir de aquí se procede de igual manera que se hizo en el ejercicio anterior.

Ovalo

Óvalo

Definición: Es una curva plana y cerrada, simétrica respecto a sus dos ejes perpendiculares y formada por cuatro arcos de circunferencia iguales dos a dos. Tiene dos ejes de simetría perpendiculares entre si 22.2.1.2 Construcción de óvalos A continuación se desarrollan algunos de los trazados de óvalos más utilizados en dibujo técnico.

Óvalo conociendo el eje menor

1. Se traza la mediatriz del eje menor CD, obteniéndose el punto O. En la mediatriz está situado el eje mayor del óvalo.

 2. Con centro en O y radio OC se dibuja una circunferencia que corta al eje mayor en los puntos O1 y O2; se unen estos puntos con C y D prolongando dichas rectas.

3. Con radio CD y centro en C y D, respectivamente, se trazan dos arcos que determinan los puntos 1 y 4, 2 y 3, puntos de tangencia entre los arcos que forman el óvalo.

 4. Por último, con centro en O1 y en O2, y radio O-1, se trazan los otros dos arcos para unir 1 con 2, y 3 con 4; de este modo queda determinado el óvalo.

Trazado de curvas tècnicas.

Trazado de curvas técnicas.

¿Qué es el trazado de curvas técnicas?

En la actualidad, una parte importante de los objetos que se fabrican están realizados bajo algún tipo de forma curva geométrica. Si prestamos atención a nuestro entorno, nos damos cuenta de que en muchos de los objetos que nos rodean están presentes las curvas técnicas y las curvas cónicas. Por ejemplo, desde la forma de parábola que algunos ojos de puente tienen, hasta la forma de ovalo u ovoide con que se han diseñado ciertas cucharas. La naturaleza también contribuye a crear este tipo de formas; los meandros de algunos ríos, o el viento al modelar las arenas de los desiertos dan testimonio de este tipo de figuras geométricas.

Curvas técnicas

Las curvas técnicas tienen muchas aplicaciones en la resolución de problemas de dibujo técnico, ya sean éstos provenientes del ámbito del diseño industrial, arquitectónico o gráfico. Las curvas de este tipo se configuran mediante la unión de arcos de circunferencia que son tangentes entre sí, dando lugar a la formación de figuras planas que pueden ser cerradas: óvalo, ovoide; o abiertas: espirales, evolvente del círculo, etcétera.